ビッグデータ（笑）を学ぼうと言う事で、似ている傾向にあるデータをどういう風に「似ている」と判断するかについて書く。

　類似度の一番基本的なものとしてユークリッド距離を使う。
　ユークリッド距離とは各アイテムを軸にとったn次元ベクトルの距離のことである。
　n次元ベクトルというとページを閉じる人が多いと思うので、最も簡単な話をする。
　二次元ベクトルでやると分かりやすい。x軸に１日の平均外出回数、ｙ軸に１日に家に滞在する時間平均を
とって「どのくらい家にひきこもってるか」の相関を作ってみる。下記の散布図が描けたとする。
　
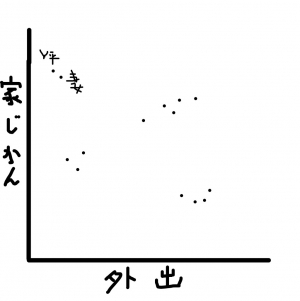
　点と点の距離が近いほど傾向が似ているのは分かるだろう。例でいえばY平さんと妻さんは傾向が似ている。
平均外出回数が極端に低く、かつ家にいる時間も長いことから引きこもりがちであると思われる。
　この点と点の距離をユークリッド距離と言う。ユークリッド距離からどの人とどの人が似ているかということを数値表示できる。今は２次元のお話しだが、これが３つの軸になって３次元になったとしても単なる点と点の距離が近いか遠いかで論じられる。
　頭の中では想像できないが４次元以上もベクトルの概念で距離が出せる。よってパラメータは２つに限らず、様々なパラメータを組み合わせて傾向が分析できるってわけ。
　さて、次に実践的なやつ。このユークリッド距離を使って自分と似ている映画ファンを探し出すアルゴリズムを考える。
　映画レビューサイトがあったとしよう。各ユーザーは自分の観た映画に対して１から５点までの評点をつける。

< /tr>

	Lady in the water	Snakes on a Plane	Just My Luck	Superman Returns	You, Me and Dupree	The Night Listener
Lisa	2.5	3.5	3.0	3.5	2.5	3.0
Gene	3.0	3.5	1.5	5.0	3.5	3.0
Michael	2.5	3.0		3.5		4.0
Claudia		3.5	3.0	4.0	2.5	4.5
Mick	3.0	4.0	2.0	3.0	3.0	2.0
Jack	3.0	4.0		5.0	3.5	3.0
Toby		4.5		4.0	1.0

　ひとりのユーザーは、最大でも６つの映画に点をつける。これを６次元ベクトルにしてユークリッド距離をはかる。映画の評点を左からy1 y2 y3 y4 y5 y6と表現し、AさんBさんのユークリッド距離（点と点の距離）の出し方は下記となる。
√（(Aさんy1)-(Bさんy1)）^2 + （(Aさんy2)-(Bさんy2)）^2 + （(Aさんy3)-(Bさんy3)）^2 + （(Aさんy4)-(Bさんy4)）^2 + （(Aさんy5)-(Bさんy5)）^2 + （(Aさんy6)-(Bさんy6)）^2
　要するに全ての平方の差を足し合わせればオッケー。
　計算面倒なのでpythonスクリプトでコーディングすると下記のような感じ。
recommendations.py

---

#-*- coding: utf-8 -*-
#!/usr/bin/env python
# A dictionary of movie critics and their ratings of a small set of movies
critics = {'Lisa Rose': {'Lady in the Water': 2.5, 'Snakes on a Plane': 3.5, 'Just My Luck': 3.0, 'Superman Returns': 3.5, 'You, Me and Dupree': 2.5, 'The Night Listener': 3.0},
'Gene Seymour': {'Lady in the Water': 3.0, 'Snakes on a Plane': 3.5, 'Just My Luck': 1.5, 'Superman Returns': 5.0, 'You, Me and Dupree': 3.5, 'The Night Listener': 3.0},
'Michael Phillips': {'Lady in the Water': 2.5, 'Snakes on a Plane': 3.0, 'Superman Returns': 3.5, 'The Night Listener': 4.0},
'Claudia Puig': {'Snakes on a Plane': 3.5, 'Just My Luck': 3.0, 'The Night Listener': 4.5, 'Superman Returns': 4.0, 'You, Me and Dupree': 2.5},
'Mick LaSalle': {'Lady in the Water': 3.0, 'Snakes on a Plane': 4.0, 'Just My Luck': 2.0, 'Superman Returns': 3.0, 'The Night Listener': 3.0, 'You, Me and Dupree': 2.0},
'Jack Matthews': {'Lady in the Water': 3.0, 'Snakes on a Plane': 4.0, 'The Night Listener': 3.0, 'Superman Returns': 5.0, 'You, Me and Dupree': 3.5},
'Toby': {'Snakes on a Plane':4.5, 'You, Me and Dupree': 1.0, 'Superman Returns': 4.0}}
from math import sqrt
# person1とperson2の距離を基にした類似性スコアを返す
def sim_distance(prefs,person1,person2):
# 二人とも評価しているアイテムのリストを得る
si={}
for item in prefs[person1]:
if item in prefs[person2]:
si[item]=1
# 両者ともに評価しているものが１つもなければ0を返す
if len(si)==0: return 0
# すべての差の平方を足し合わせる
sum_of_squares = sum([pow(prefs[person1][item] - prefs[person2][item], 2) for item in si])
return 1/(1+sum_of_squares)

---

　このスクリプトは、recommendations.sim_distance(recommendations.critics, Aさんの名前, Bさんの名前)とpythonで実行すると、AさんBさんのユークリッド距離を出してくれて、それの１プラスした逆数を出してくれる。

---

# すべての差の平方を足し合わせる
sum_of_squares = sum([pow(prefs[person1][item] - prefs[person2][item], 2) for item in si])
return 1/(1+sum_of_squares)

---

　距離が０であれば逆数は１となる。つまり１に近いほど類似度が高いということを表す。
　これを使ってLisa Roseさんが誰と一番類似しているかを出す。

>>> import recommendations
>>> recommendations.sim_distance(recommendations.critics, ‘Lisa Rose’, ‘Gene Seymour’)
0.14814814814814814
>>> recommendations.sim_distance(recommendations.critics, ‘Lisa Rose’, ‘Michael Phillips’)
0.4444444444444444
>>> recommendations.sim_distance(recommendations.critics, ‘Lisa Rose’, ‘Claudia Puig’)
0.2857142857142857
>>> recommendations.sim_distance(recommendations.critics, ‘Lisa Rose’, ‘Mick LaSalle’)
0.3333333333333333
>>> recommendations.sim_distance(recommendations.critics, ‘Lisa Rose’, ‘Jack Matthews’)
0.21052631578947367
>>> recommendations.sim_distance(recommendations.critics, ‘Lisa Rose’, ‘Toby’)
0.2222222222222222

実行の結果、Michael Phillipsさんが一番１に近くなっていて類似していることが分かる。
　一番基本のやり方であるが、このやり方であればどんな人の趣味思考が似てるかってのをビッグデータ（笑）を使って数値表現できる。
　ただこれでは自分が出したい類似性ってのが出せない場合がある。それはまた次回。
　ちなみに今回の話は下記の「集合値プログラミング」の2.3.1章のお話が詳しい。ためになり読みやすい本。pythonが使えればより色んなビッグデータ的事例を楽しくプログラミング出来る。しかもすげえ実践的なためたぶん即使える。今後もこれベースで学習していく。

【ニコ動でゲーム実況してました。】
ニコニコ動画ゲーム実況一覧
【twitter】気軽にフォローしてください→@yhei_hei